Macroeconomic Policy & Extreme Shocks
Week 10
November 18, 2025
1. Fed’s Dual Mandate (Again)
The Fed’s Dual Mandate
The Fed’s dual mandate according to the Federal Reserve Bank of Chicago
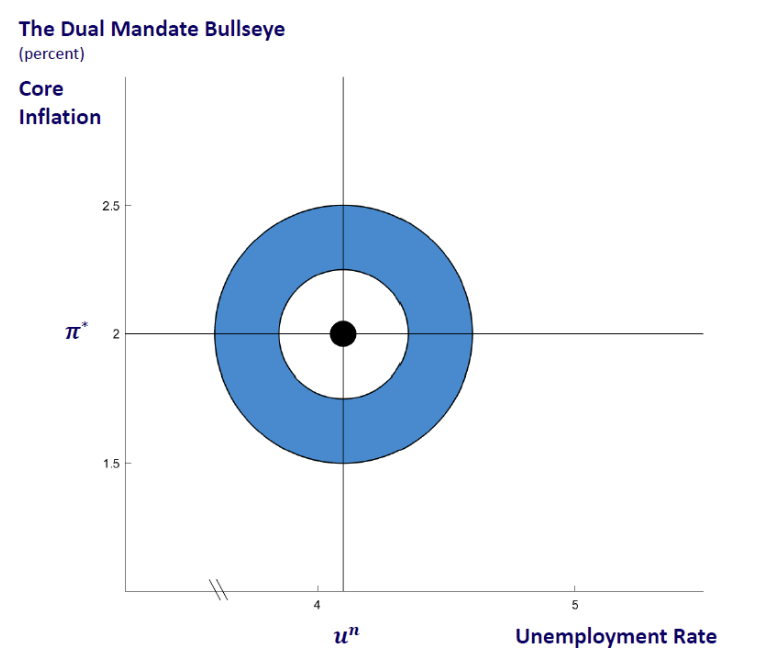
The FRB of Chicago calls the target inflation rate by \(\pi^*\)
We call it \(\pi^{_T}\)
The meaning is the same
2. Inflation Targeting
Inflation Rate Target
All central banks in advanced countries have an optimal value for inflation they want to achieve. This is called the inflation target:\[\color{blue}{\pi^{_T}}\]
\(~~~~~~~~~~~~~~~~~~~~~\)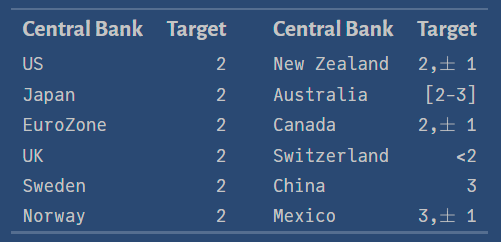
Source: Central Bank News
Targeting Inflation: Two Ways to Do It
There are two different ways of looking at the target value:
- \(\pi^{_T}\) is a ceiling. The central bank suffers a loss if \(\pi>\pi^{_T}\)
- \(\pi^{_T}\) as a true target . The central bank suffers a loss if \(\pi \neq \pi^{_T}\).
Examples:
- Ceiling: Switzerland (still now), ECB (until July 2021)
- True Target: all central banks in advanced economies
What’s The Problem With \(\pi^{_T}\) as a Ceiling?
- If \(\pi^{_T}\) is used as a ceiling, central banks will be biased to keep inflation systematically below the target.
- It may lead to “too low inflation” or even deflation
- The costs to the society will be higher than if the target were reached
- ECB changed its monetary policy strategy in July 2021 for that reason:
European Central Bank, 8 July 2021:
“The Governing Council considers that price stability is best maintained by aiming for a 2% inflation target over the medium term. This target is symmetric, meaning negative and positive deviations of inflation from the target are equally undesirable.”
3. The Taylor Rule
The Textbook Rule
How the textbook rule performs, compared with the Fed Funds Rate?
We may recall our well-known MP curve (rule) and the Fisher equation: \[ r=\bar{r}+\lambda \cdot \pi \tag{MP curve} \] \[ i=\pi+r \tag{Fisher eq.} \]
Insert the MP in the Fisher eq., and the Fed funds rate \((i)\) comes out as: \[ i=\bar{r}+\pi+\lambda \cdot \pi \]
Using data on \(\overline{r}, \pi, \lambda\), we can calculate \(i\) from this rule.
Then, we can compare this \(i\) with the Fed Funds Rate that the Fed sets over time.
See the following figure.
The Textbook Rule vs the Fed Funds Rate
We set: \(\lambda=0.5, \overline{r}=2\). The textbook rule performs very badly.
Policy Rules & How Policymakers Use Them
- The MP rule studied in previous weeks was helpful in explaining the basic concepts in macroeconomics.
- However, in reality, central banks use a more sophisticated rule for making decisions about \((i)\).
- The other items always included in the rule are:
- The target inflation rate
- The output-gap
- A trending factor to consider inertia (not covered here)
- We can check the the different types of rules used by the Fed here: Policy Rules and How Policymakers Use Them
The Taylor Rule’s New Elements
John Taylor (1993) proposed a more comprehensive rule that includes the inflation gap:1 \[ \pi^{g a p}=\pi-\pi^{_T} \]
… and the output gap: \[ Y^{g a p}=\frac{Y-Y^P}{Y^P} \]
Output gap is usually expressed in percentage points \((+2 \%,-1 \%, \ldots)\)2
The Taylor Rule
The Taylor rule gives the nominal interest rate set by the central bank as: \[ i=\overline{r}+\pi+\lambda \cdot \pi^{g a p}+\lambda \cdot Y^{g a p} \tag{1} \]
As the Fisher equation gives us: \[ i=\pi+r \tag{2} \]
Equalizing eq. (1) and (2), we get the real interest rate that results from the intervention of the central bank: \[ r=\overline{r}+\lambda \cdot \pi^{g a p}+\lambda \cdot Y^{g a p} \tag{3} \]
Finally, Taylor proposes the following values for the exogenous variables: \[ \overline{r}=2 \% \ \ , \ \pi^{_T} =2 \% \]
The Taylor Rule vs the Fed Funds Rate
Weights: 0.5 for the output-gap, 0.5 for the inflation-gap.
The New Taylor Rule vs the Fed Funds Rate
Weights: 1.0 for the output-gap, 0.5 for the inflation-gap: it performs better
Taylor Rule on Autopilot?
Why hasn’t the Fed put the federal funds rate on a Taylor rule autopilot ?
- Recall the logic behind rules in monetary policy:
- No rules leave room for speculation, higher uncertainty, and risk.
- Too strict rules leave room for too much punishment.
- It is a balance between some guiding rule and a flexible implementation of such rule that leads to the best possible outcome.
- The Taylor rule may be pretty helpful in “normal” situations.
- But exceptional circumstances can only be dealt with exceptional measures.
- Great Recession in 2008-2011
- COVID pandemic in 2020-21
- Galloping oil prices and the war in Ukraine in 2022-23.
4. Strange Times:
– From the Fear of Deflation to Galloping Inflation –
Living Through Strange Times
Over the last 15 years, we have lived under two extreme situations:
- Explosive inflation: from mid 2021 to mid 2023
- Fear of deflation: from 2008 up to 2021
Terrible shocks hit Western economies:
- A financial crisis of a monumental scale in 2008-2011
- Oil prices increasing at rates well over 200% per year
- Covid19 pandemic
- War in Ukraine
Living Through Strange Times
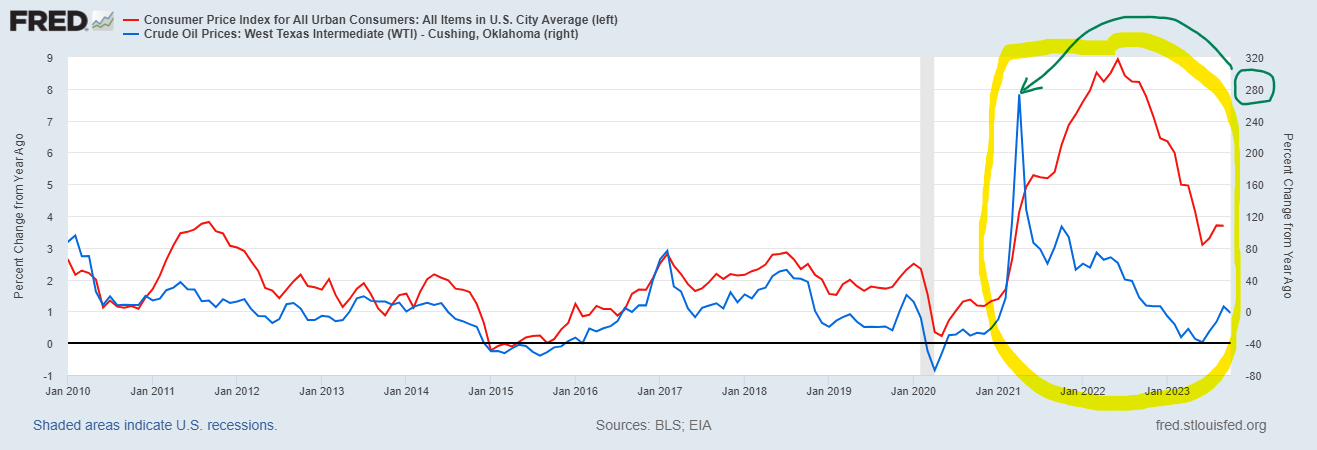
Explosive Inflation
- In Western countries, inflation reached very high levels … very fast
How to Deal With Explosive Inflation?
In the summer of 2022, it was very “fashionable” to argue that the only way to control explosive inflation was to cause a severe recession.
For example, a very influential economist, Larry Summers, defended that:
“We need five years of unemployment above 5% to contain inflation – in other words, we need two years of 7.5$ unemployment or five years of 6% unemployment or one year of 10% unemployment.” speech in London, 20 June 2022. Bloomberg
Summers was not alone: there was quite a large chorus on this camp.
Fortunately, their predictions proved wrong: inflation has been coming down and unemployment has not gone up!
The Fear of Deflation
- 20 years ago, it was inconceivable to think that nominal interest rates could be \(0 \%\) or even negative.
- However, in the summer of 2021 they were negative in many countries (Switzerland, Euro Zone, Japan, Denmark, Sweden).
- In the US, the Fed made a decision: to cut nominal interest rates as much as possible, but they would stop at the \(0 \%\) limit.
- Not going below \(0 \%\), is what we mean by the Zero Lower Bound on \((i)\).
Switzerland: Pinnacle of Financial Stability
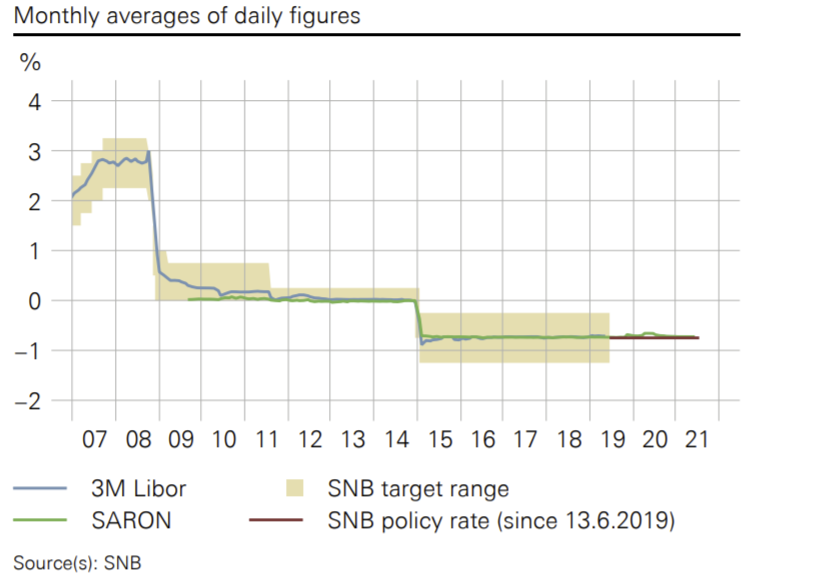
- The Swiss National Bank (SNB) kept the interest rate at \(-0.75 \%\) for a long time.
- In September 2022, the SNB decided to raise the rate to \(+0.5 \%\).
EURIBOR: The Unthinkable
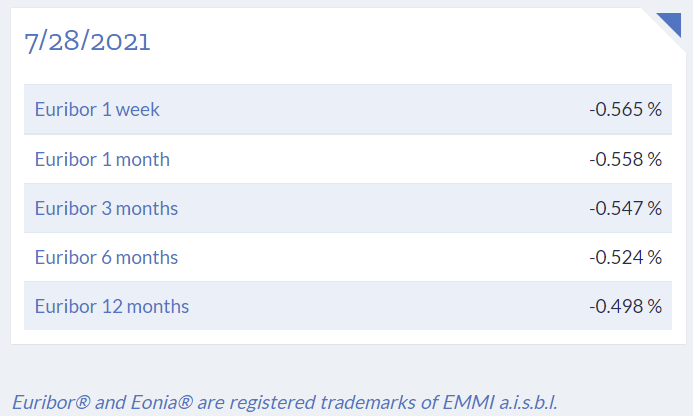
- Euribor rates were negative (for all maturities) in the summer of 2021.
- Currently, they range from \(2.4\%\) and \(2.6\%\)
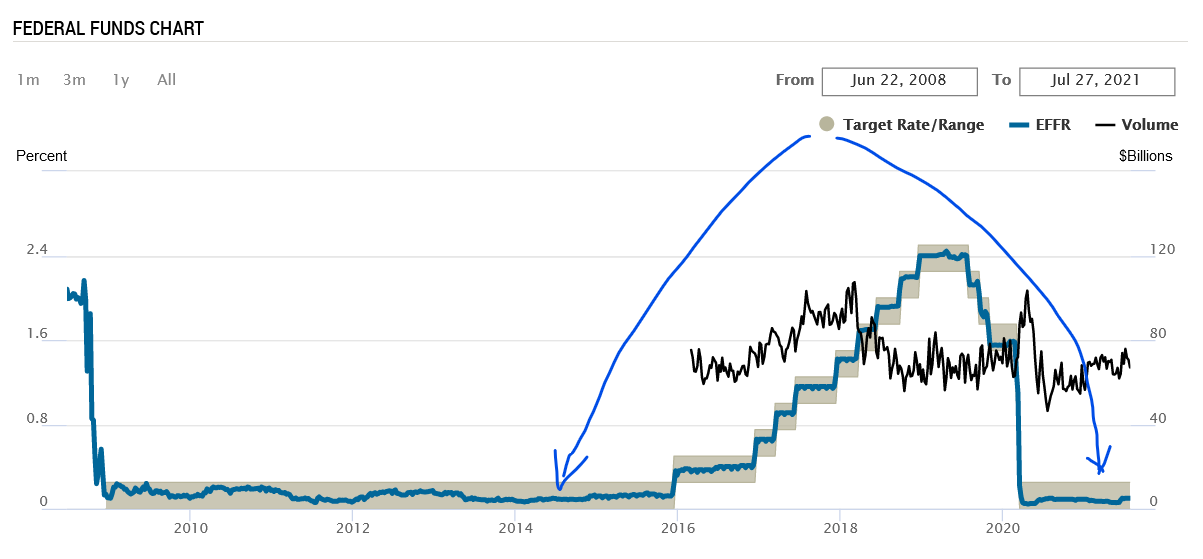
The ZLB: the US case
The Fed Funds Rate is the blue line (it is the overnight market rate); the FED sets the range (the gray interval) in the lower limit (0%). FRB of New York
ZLB: Consequences
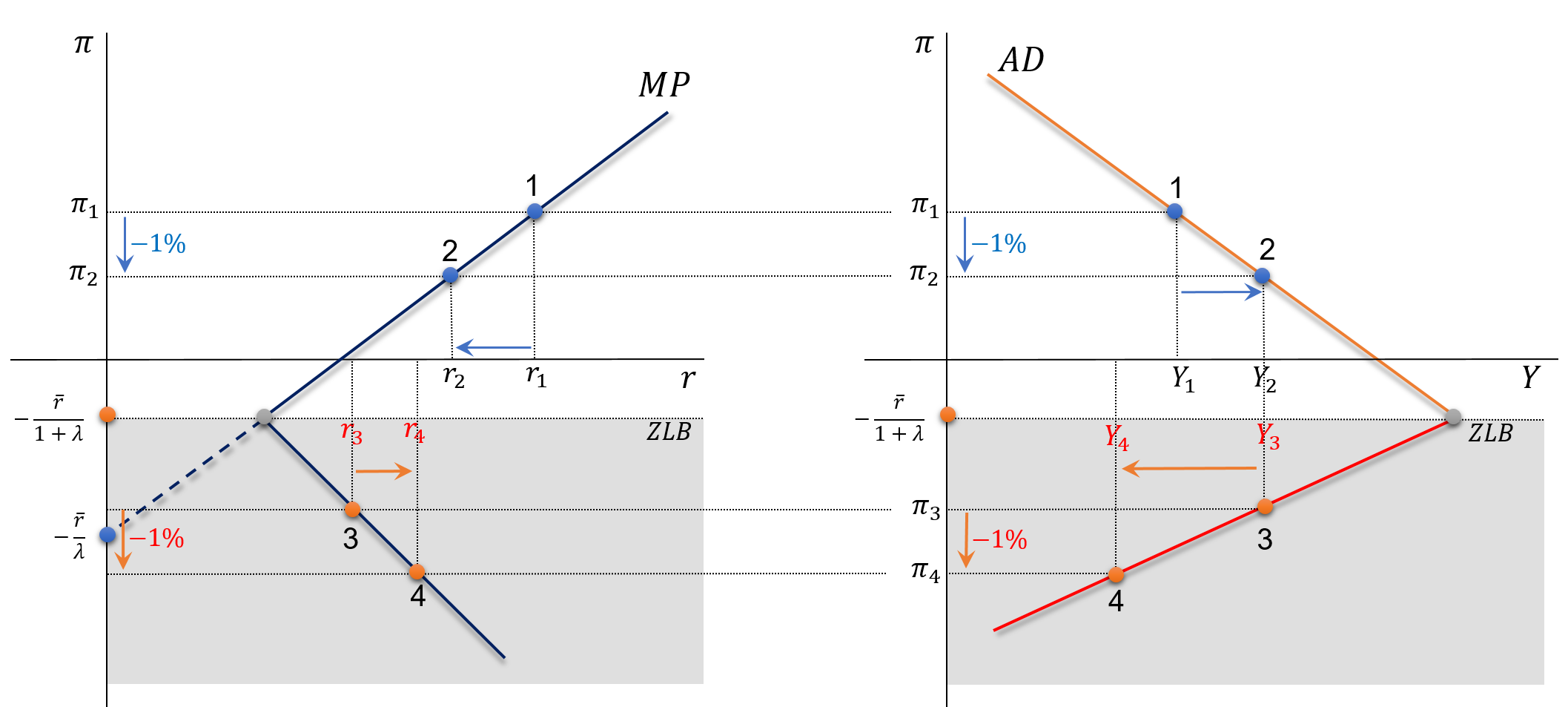
- Until the ZLB is reached, the MP and AD curves have their normal representations.
- However, when the ZLB is reached, there will be a kink in those two curves, and their slopes become the opposite of what they were.
- This has dramatic consequences for:
- The macroeconomic equilibrium
- GDP, inflation and unemployment
- The way monetary policy is conducted
- The way fiscal policy is used as a policy tool
ZLB: Representation of the MP curve
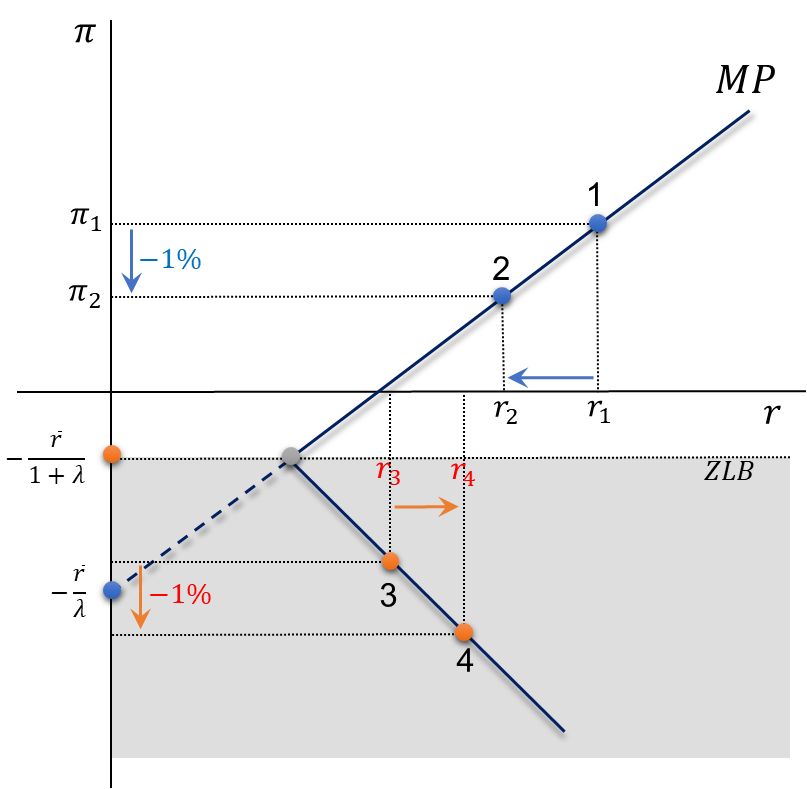
- MP in the normal zone: \[r=\overline{r}- \lambda \pi\]
- MP in the ZLB: \[r=-\pi_{_{ZL}}\]
ZLB: Representation of the AD curve
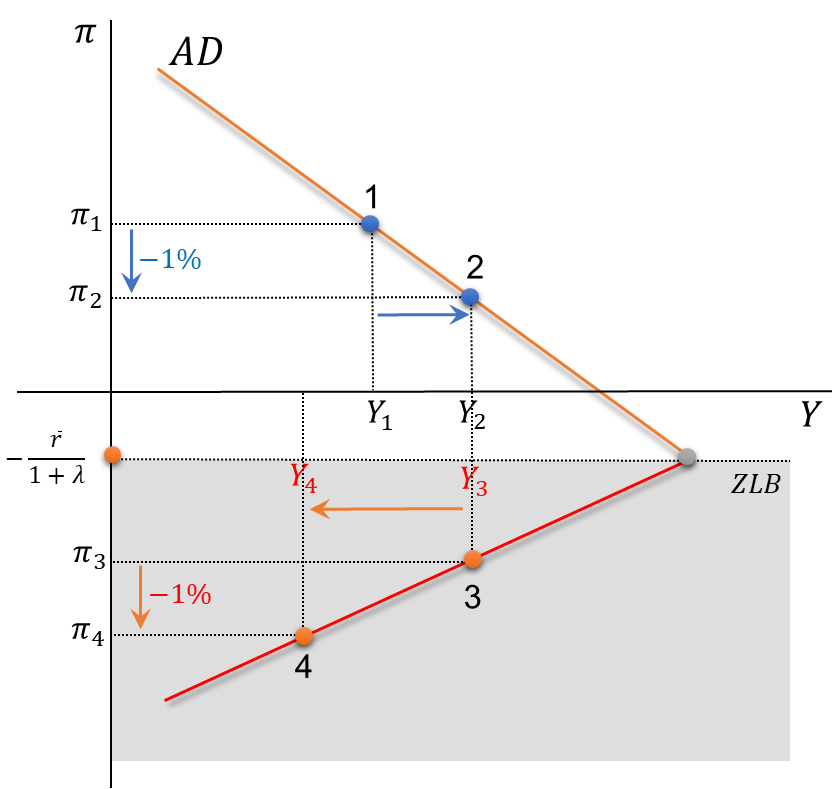
- AD in the normal zone: \[Y=m \cdot \overline{A}-m \cdot \phi \cdot(\overline{r}+\lambda \pi)\]
- AD in the ZLB: \[Y=m \cdot \overline {A}+m \cdot \phi \cdot \pi_{_{Z L}}\]
ZLB: Representation of AD and MP Curves
A reduction in inflation of \(1 \%\) causes different (opposite) impacts upon \(Y\) and \(r\) when comparing the ZLB with the normal zone.
5. Strange Things Happen in the ZLB
Not covered in this course.
Alice Trough the Looking Glass
Paul Krugman, Nobel Prize winner 2008: the ZLB is a “Alice through the looking glass” experience.

Strange Things I: Deflation Trap
Suppose the economy falls into the ZLB (point \(1_{Z L}\) ). It will end up in the long-term equilibrium \(2_{Z L}\) and remain trapped there forever.
Previous Slide’s Details: Read at Home
Consider that, for some reason, the economy is operating at point \(1_{Z L}\) in the ZLB. This point is determined by the intersection of the AD curve (which in the ZLB we call by ADzl) and the initial AS curve (AS1).
At point \(1_{_{Z L}}\), the economy has negative inflation \((\pi=-3.6 \%, Y=13.4)\), \(Y^P=14\) trillion dollars. This point represents a short-run equilibrium but not a long-run one because we are in a recession.
In a recession, inflation is forced to come down, which will shift the AS to the right (AS1->AS2). This movement will only stop when the recession is eliminated by declining inflation, which occurs when the AS2 crosses the ADzl at point \(2_{Z L}\).
Point \(2_{_{Z L}}\) represents the long-term equilibrium for this economy, with \((\pi=-2 \%)\), and \(Y=Y^P=14\). The economy will be stuck at this equilibrium forever until some new major shock forces it to move away from such a trap.
This case looks like what has happened to Japan since the late 1990s.
Strange Things II: Secular Stagnation
Suppose a big negative demand shock forces the economy to move to point 2. In the long term, it will end up at point 3.
Previous Slide’s Details: Read at Home
Consider the economy is operating at point 1, with inflation of \(\pi_1=2 \%\) and \(Y=Y^P=14\) trillion dollars: it is a long-run equilibrium.
Suppose that the AD suffers a huge negative shock and the economy moves to point 2. This point is not a long-run equilibrium because we are in a large recession.
In a recession, inflation decreases, and the AS shifts to the right. The economy moves to point 3.
At point 3, demand is insufficient to match supply at a higher GDP level. So GDP is stuck at a level that is permanently lower than what the economy can produce ( \(Y^P=14\) ). Only very aggressive monetary and fiscal expansionary policies can (by forcing a large increase in AD ) remove the economy from such stagnation.
Appendix 1: Derivation of the ZLB
Not compulsory; Not included in TESTS/EXAMS.
Appendix 1: Derivation of the ZLB
From the Fisher equation we have \[ r=i-\pi\tag{4} \]
From the MP curve we have \[ r=\overline{r}+\lambda \pi \tag{5} \]
Equalizing eq. (4) and (5), and imposing the ZLB condition \((i=0)\), we get the inflation rate that corresponds to the ZLB: \[ \overline{r}+\lambda \pi=\underbrace{i}_{=0}-\pi \quad \Rightarrow \quad \pi_{_{Z L}}=-\frac{\overline{r}}{1+\lambda} \tag{6} \]
Therefore, from (6) we can obtain \[ \overline{r}=-(1+\lambda) \pi_{_{Z L}} \tag{7} \]
Appendix 1: Derivation of the ZLB (contin.)
Now, substitute eq. (7) into eq. (5), and we will obtain \[r=-(1+\lambda) \pi_{_{ZL}}+\lambda \pi_{_{_ZL}} \quad \Rightarrow \quad r=-\pi_{_{_ZL}} \tag{8}\]
Surprisingly, as in the ZLB \((i=0 \%)\), the MP curve acquires a negative slope. \[r=-\pi_{_{Z L}} \tag{9}\]
with values for inflation in the ZLB such that \[ \pi_{_{_ {ZL}}} \leq-\frac{\bar{r}}{1+\lambda} \tag{10} \]
Readings
Readings
Read Chapter 13 of the adopted textbook:
Frederic S. Mishkin (2015). Macroeconomics: Policy & Practice, Second Edition, Pearson Editors.
